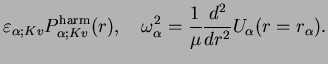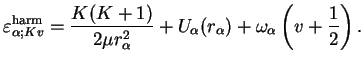Next: The Energy Spectrum
Up: Radial SE
Previous: Radial SE
Contents
Index
The rotation term
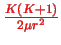 is assumed as small, and the potential
is assumed as small, and the potential
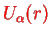 is expanded around a minimum
is expanded around a minimum
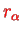 ,
,
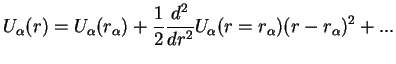 |
|
|
(1.29) |
Here,
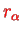 can be considered as the equilibrium distance of the two nuclei which clearly still depends on the electronic quantum number
can be considered as the equilibrium distance of the two nuclei which clearly still depends on the electronic quantum number
 .
If the higher order terms in the Taylor expansion are neglected, and
.
If the higher order terms in the Taylor expansion are neglected, and
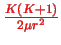 replaced by
replaced by
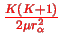 , the approximate SE becomes
, the approximate SE becomes
This is the equation of a linear harmonic oscillator apart from the fact that
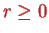 . However,
. However,
 has been assumed to be small anyway and within this approximation, the energy levels are therefore those of a linear harmonic oscillator shifted by
has been assumed to be small anyway and within this approximation, the energy levels are therefore those of a linear harmonic oscillator shifted by
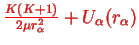 ,
,
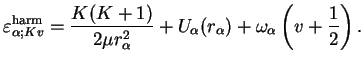 |
|
|
(1.31) |





Next: The Energy Spectrum
Up: Radial SE
Previous: Radial SE
Contents
Index
Tobias Brandes
2005-04-26
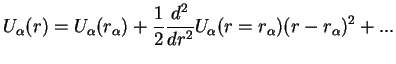
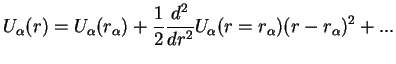
![$\displaystyle \left[ -\frac{1}{2\mu}\frac{d^2}{dr^2} + \frac{K(K+1)}{2\mu r_\al...
...rac{1}{2}\mu \omega_\alpha^2 (r-r_\alpha)^2 \right] P^{\rm harm}_{\alpha;Kv}(r)$](img1410.png)