Exact solution

We find the exact eigenvectors $\vert{i}\rangle$ and eigenvalues $\varepsilon_{i}$ of ${\mathcal H}_{\rm TLS}$, that is the solutions of

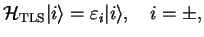$${\mathcal H}_{\rm TLS}\vert{i}\rangle = \varepsilon_{i} \vert{i}\rangle,\quad i=\pm ,$$ (2.4)

by diagonalisation of the two-by-two matrix Eq. (II.2.3). The eigenstates $\vert\pm\rangle$ and eigenvalues $\varepsilon_{\pm}$ of ${\mathcal H}_{\rm TLS}$ are

$$\vert\pm \rangle = \frac{1}{N_{\pm}}\left[ \pm 2T_c \vert L\rangle + (\Delta \mp \va... ...t R\rangle \right],\quad N_{\pm}\equiv \sqrt{4T_c^2+(\Delta \mp \varepsilon)^2}$$

$$\varepsilon_{\pm} = \pm \frac{1}{2}\Delta,\quad \Delta\equiv\sqrt{\varepsilon^2+4T_c^2},$$ (2.5)

corresponding to hybridized wave functions, i.e. bonding and anti-bonding superpositions of the two, originally localized states $\vert L\rangle$ and $\vert R\rangle$. The corresponding eigenvalues $\varepsilon_{\pm}=\pm \frac{1}{2}\Delta$ of the double well represent two energy surfaces over the $T_c$- $\varepsilon$ plane, with an avoided level crossing of splitting $\Delta$. For $\varepsilon=0$, one has $\vert\pm \rangle=(1/\sqrt{2})(\pm {\rm sign}(T_c)\vert L\rangle + \vert R\rangle )$ such that for the choice $T_c<0$ the ground state $\vert-\rangle = (1/\sqrt{2}) (\vert L\rangle + \vert R\rangle )$ with energy $\varepsilon_-=-\frac{1}{2}\Delta$ is the symmetric superposition of $\vert L\rangle$ and $\vert R\rangle$.

Figure: New hybridized basis states of the double well potential.

Exercise: Check these results by doing the diagonalisation! Hint: this leads to a quadratic equation.