Second Order Perturbation Theory

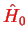If $E_i$ is a (non-degenerate) eigenvalue of $\hat{H}_0$ with (normalised) eigenvector $\vert i\rangle$, the second order approximation $E_i^{(2)}$ of the corresponding new eigenvalue of $\hat{H}_0+\hat{H}_1$ is given by

$${\color{col1}E_i^{(2)} = E_i + \langle i \vert \hat{H}_1 \vert i ... ...i\ne j} \frac{\vert\langle i \vert \hat{H}_1 \vert j \rangle \vert^2}{E_i-E_j}}$$ (2.6)

Note that in our case here the unperturbed states are $\vert i=1\rangle = \vert L\rangle$ and $\vert i=2\rangle = \vert R\rangle$, and the energies are $E_1=\varepsilon/2$ and $E_2=-\varepsilon/2$. We have $\langle i \vert \hat{H}_1 \vert i \rangle =0$ whence the first order correction vanishes. We furthermore have

$$\langle L \vert \hat{H}_1\vert R \rangle = \langle R \vert \hat{H}_1 \vert L \rangle =T_c,$$ (2.7)

which leads to

$$E_1^{(2)} = \frac{\varepsilon}{2} + \frac{T_c^2}{E_1-E_2}= \frac{\varepsilon}{2} + \frac{T_c^2}{\varepsilon}$$ (2.8)

$$E_2^{(2)} = -\frac{\varepsilon}{2} + \frac{T_c^2}{E_2-E_1}= -\frac{\varepsilon}{2} - \frac{T_c^2}{\varepsilon}.$$ (2.9)

We compare this to a Taylor expansion of the exact result, Eq. (II.2.4), for the eigenvalues $\varepsilon_\pm$:

$$\varepsilon_{\pm} = \pm \frac{1}{2}\sqrt{\varepsilon^2+4T_c^2} = \pm \frac{1}{2}\vare... ...2 \frac{T_c^2}{\varepsilon^2} + O\left(\frac{T_c}{\varepsilon}\right)^4\right],$$ (2.10)

which means that

$$\varepsilon_+ = \frac{1}{2}\varepsilon + \frac{T_c^2}{\varepsilon}+ O\left(\frac{... ...arepsilon - \frac{T_c^2}{\varepsilon}+ O\left(\frac{T_c}{\varepsilon}\right)^4,$$ (2.11)

which co-incides with our perturbation theory, i.e. the expressions Eq. (II.2.8) for $E_1^{(2)}$ and $E_2^{(2)}$! At the same time, we make the following observations:

• the perturbative result is good for a `small' perturbation: in our case here, this means that the parameter $T_c/\varepsilon$ has to be small in order to justify neglecting the $O\left(\frac{T_c}{\varepsilon}\right)^4$ terms.
• If $T_c/\varepsilon$ becomes too large, the perturbation expansion breaks down: the Taylor series for $\sqrt{1+x}$ converges only for $\vert x\vert<1$. Here, $x=4T_c/\varepsilon$ such that $4T_c/\varepsilon<1$ must be fulfilled.
• Large $T_c$ means strong coupling between the left and right `mini-atom' and therefore strong bonding between these two atoms into a new, quantum mechanical unit: a molecule. This molecule bonding can therefore, stricly speaking, not be calculated from perturbation theory in $T_c$ (fortunately, we have the exact solution). In many `real-world' cases, however, an exact solution is not available and one has to approach the problem from a different angle in order to avoid simple-minded perturbation theory. This is what P. W. Anderson probably meant in a popular science article some years ago, with the (intentionally) slightly provocative title `Brain-washed by Feynman ?' (Feynman diagrams represent perturbation theory).

Backup literature for this section: textbook Gasiorowisz [3] cp. 11 for time-independent perturbation theory (revise if necessary). Lecture notes QM 1 chapter 3

http://brandes.phy.umist.ac.uk/QM/http://brandes.phy.umist.ac.uk/QM/ for two-level system.