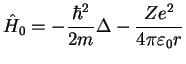Next: Kinetic Energy and Darwin
Up: Some Revision, Fine-Structure of
Previous: Second Order Perturbation Theory
Contents
Index
The fine structure is a result of relativistic corrections to the Schrödinger equation, derived from the relativistic Dirac equation for an electron of mass
 and charge
and charge
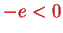 in an external electrical field
in an external electrical field
 . Performing an expansion in
. Performing an expansion in
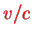 , where
, where
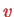 is the velocity of the electron and
is the velocity of the electron and
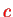 is the speed of light, the result for the Hamiltonian
is the speed of light, the result for the Hamiltonian
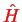 can be written as
can be written as
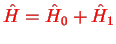 ,
where
,
where
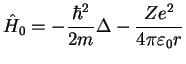 |
|
|
(3.1) |
is the non-relativistic Hydrogen atom, (
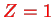 ), cf. Eq. (II.1.7), and
), cf. Eq. (II.1.7), and
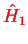 is treated as a
perturbation to
is treated as a
perturbation to
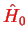 , using perturbation theory.
, using perturbation theory.
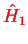 consists of three terms: the kinetic energy correction, the Darwin term, and the Spin-Orbit coupling,
consists of three terms: the kinetic energy correction, the Darwin term, and the Spin-Orbit coupling,
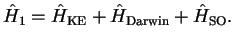 |
|
|
(3.2) |
Literature: Gasiorowicz [3] cp. 12 (Kinetic Energy Correction, Spin-Orbit coupling); Weissbluth [4] (Dirac equation, Darwin term); Landau Lifshitz Vol IV chapter. 33,34.
Subsections





Next: Kinetic Energy and Darwin
Up: Some Revision, Fine-Structure of
Previous: Second Order Perturbation Theory
Contents
Index
Tobias Brandes
2005-04-26