




Next: Permutations
Up: Introduction into Many-Particle Systems
Previous: Introduction into Many-Particle Systems
Contents
Index
In Quantum Mechanics, a system of
 particles with internal spin degrees of freedom
particles with internal spin degrees of freedom
 is described by a wave function which in the position representation reads
is described by a wave function which in the position representation reads
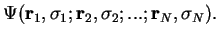 |
|
|
(1.1) |
Here,
 is the probability density for finding particle 1 at
is the probability density for finding particle 1 at
 with spin quantum number(s)
with spin quantum number(s)
 , particle 2 at
, particle 2 at
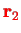 with spin quantum number(s)
with spin quantum number(s)
 ,... etc. Note that for spin
,... etc. Note that for spin
 , one would choose for
, one would choose for
 one of the spin projections, e.g.
one of the spin projections, e.g.
 .
.
Remark: Usually, many-particle wave functions and the issue of indistinguishability are discussed in the position representation.
Subsections
Tobias Brandes
2005-04-26