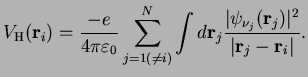Next: Angular Average, Shells, and
Up: The Hartree Equations, Atoms,
Previous: The Hartree Equations, Atoms,
Contents
Index
The basic idea here is to replace the complicated interactions among the electrons by an effective, average potential energy that each electron
 at position
at position
 experiences.
experiences.
In the Hartree approach one assumes that particle
 is described by a wave function (spin orbital)
is described by a wave function (spin orbital)
 with orbital part
with orbital part
 , and the statistics (anti-symmetrization of all the total
, and the statistics (anti-symmetrization of all the total
 -particle wave function for Fermions, symmetrizatin for Bosons) is neglected. In the following, we discuss electrons.
-particle wave function for Fermions, symmetrizatin for Bosons) is neglected. In the following, we discuss electrons.
For electrons interacting via the Coulomb interaction
 , the potential seen by an electron
, the potential seen by an electron
 at position
at position
 is given by
is given by
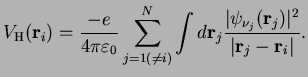 |
|
|
(1.1) |
This is the sum over the potentials generated by all other electrons
 which have a charge density
which have a charge density
 . The corresponding potential energy for electron
. The corresponding potential energy for electron
 is
is
 , and therefore one describes electron
, and therefore one describes electron
 by an effective single particle Hamiltonian,
by an effective single particle Hamiltonian,
where
 is the usual potential energy due to the interaction with the nucleus. The corresponding Schrödinger equations for the orbital wave functions
is the usual potential energy due to the interaction with the nucleus. The corresponding Schrödinger equations for the orbital wave functions
 for electron
for electron
 are
are
![$\displaystyle \left[ -\frac{\hbar^2}{2m}\Delta_i+ V({\bf r}_i)+\frac{e^2}{4\pi\...
..._i\vert}\right] \psi_{\nu_i}({\bf r}_i)=
\varepsilon_i \psi_{\nu_i}({\bf r}_i).$](img530.png) |
|
|
(1.3) |
The total wave function in this Hartree approximation is the simple product
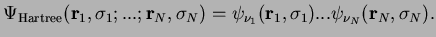 |
|
|
(1.4) |
Remarks:
- The Hartree equation Eq. (IV.1.3) is a set of
 non-linear coupled integro-differential equations.
non-linear coupled integro-differential equations.
- As the solutions
 of the equations appear again as terms (the Hartree potential) in the equations, these are called self-consistent equations. One way to solve them is by iteration: neglect the Hartree term first, find the solutions
of the equations appear again as terms (the Hartree potential) in the equations, these are called self-consistent equations. One way to solve them is by iteration: neglect the Hartree term first, find the solutions
 , insert them in the Hartree potential, solve the new equations for
, insert them in the Hartree potential, solve the new equations for
 , insert these again, and so on until convergence is reached.
, insert these again, and so on until convergence is reached.
- The Pauli principle is not properly accounted for in this approach, as we do not have a Slater determinant but only a product wave function. This can be improved by the Hartree-Fock equations which we derive in the next section.





Next: Angular Average, Shells, and
Up: The Hartree Equations, Atoms,
Previous: The Hartree Equations, Atoms,
Contents
Index
Tobias Brandes
2005-04-26
![]() is described by a wave function (spin orbital)
is described by a wave function (spin orbital)
![]() with orbital part
with orbital part
![]() , and the statistics (anti-symmetrization of all the total
, and the statistics (anti-symmetrization of all the total
![]() -particle wave function for Fermions, symmetrizatin for Bosons) is neglected. In the following, we discuss electrons.
-particle wave function for Fermions, symmetrizatin for Bosons) is neglected. In the following, we discuss electrons.
![]() , the potential seen by an electron
, the potential seen by an electron
![]() at position
at position
![]() is given by
is given by