




Next: Periodic Table
Up: The Hartree Equations, Atoms,
Previous: Effective Average Potential
Contents
Index
A further simplification of the Hartree equations, Eq. (IV.1.3), is achieved by replacing the Hartree potential by its angular average,
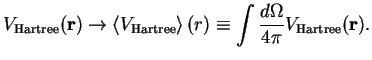 |
|
|
(1.5) |
This still depends on all the wave functions
 , but as the one-particle potential now is spherically symmetric, we can use the decomposition into spherical harmonics, radial wave functions, and spin,
, but as the one-particle potential now is spherically symmetric, we can use the decomposition into spherical harmonics, radial wave functions, and spin,
 |
|
|
(1.6) |
Here, the index
 indicates that we are back to our usual quantum numbers
indicates that we are back to our usual quantum numbers
 that we know from the hydrogen atom. In contrast to the latter, the radial functions now depend on
that we know from the hydrogen atom. In contrast to the latter, the radial functions now depend on
 and
and
 because we do not have the simple
because we do not have the simple
 Coulomb potential as one-particle potential.
Coulomb potential as one-particle potential.
An even cruder approximation to
 would be a parametrization of the form
would be a parametrization of the form
by which one loses the self-consistency and ends up with one single Schrödinger equation for a particle in the potential
 .
.
Exercise: Give a physical argument for the condition
 in the above equation.
in the above equation.
Subsections





Next: Periodic Table
Up: The Hartree Equations, Atoms,
Previous: Effective Average Potential
Contents
Index
Tobias Brandes
2005-04-26
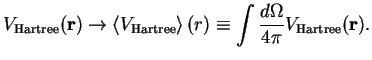
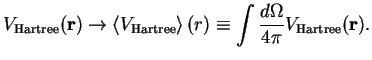
![]() would be a parametrization of the form
would be a parametrization of the form


![]() in the above equation.
in the above equation.