




Next: Hamiltonian for Fermions
Up: Angular Average, Shells, and
Previous: Angular Average, Shells, and
Contents
Index
The ground states of atoms with
 electrons in the period table can now be understood by forming Slater determinants (`configurations') with
electrons in the period table can now be understood by forming Slater determinants (`configurations') with
 spin-orbitals
spin-orbitals
 . The atoms are thus `built up' from these solutions. This is denoted as
. The atoms are thus `built up' from these solutions. This is denoted as
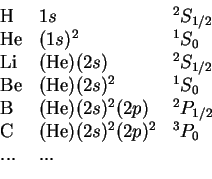 |
|
|
(1.9) |
These are built up by `filling up the levels' with electrons. For a given
 there are
there are
 orbitals (2 spin states for each given
orbitals (2 spin states for each given
 -value).
-value).
The spectroscopic description is given by the quantum numbers
 ,
,
 ,
,
 (total spin, orbital, angular momentum) in the form
(total spin, orbital, angular momentum) in the form
 |
|
|
(1.10) |
Carbon is the first case where Hund's Rules kick in. These `rules' are rules and no strict theorems, but they seem to work well for the understanding of atoms. Here I cite them after Gasiorowicz (web-supplement)
- The state with largest
 lies lowest: spin-symmetric WFs have anti-symmetric orbital WFs and therefore reduced electron-electron interaction.
lies lowest: spin-symmetric WFs have anti-symmetric orbital WFs and therefore reduced electron-electron interaction.
- For a given value of
 , the state with maximum
, the state with maximum  lies lowest: the higher
lies lowest: the higher  , the more lobes (and thereby mutual `escape routes' for interacting electrons) there are in the
, the more lobes (and thereby mutual `escape routes' for interacting electrons) there are in the  s.
s.
 ,
,  given. (i) not more than half-filled incomplete shell:
given. (i) not more than half-filled incomplete shell:  ; (ii) more than half-filled shell:
; (ii) more than half-filled shell:  : due to spin-orbit interaction.
: due to spin-orbit interaction.





Next: Hamiltonian for Fermions
Up: Angular Average, Shells, and
Previous: Angular Average, Shells, and
Contents
Index
Tobias Brandes
2005-04-26
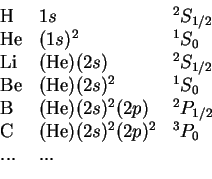
![]() ,
,
![]() ,
,
![]() (total spin, orbital, angular momentum) in the form
(total spin, orbital, angular momentum) in the form