




Next: Expectation value of
Up: The Hartree-Fock Method
Previous: Periodic Table
Contents
Index
This is a preparation for the new method (Hartree-Fock) we learn in the next section where we deal with interactions between a large number of Fermions.
The Hamiltonian for
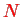 Fermions is given by the generalization of the
Fermions is given by the generalization of the
 case, Eq. (III.2.17), and reads
case, Eq. (III.2.17), and reads
Subsections
Tobias Brandes
2005-04-26
![]() Fermions is given by the generalization of the
Fermions is given by the generalization of the
![]() case, Eq. (III.2.17), and reads
case, Eq. (III.2.17), and reads