Expectation value of $\hat{U}$

This is only slightly more complicated: consider for example the term $U(\xi_1,\xi_2)$,

$$\langle \Psi \vert U(\xi_1,\xi_2)\vert \Psi\rangle= \frac{1}{N!}\... ...}\nu_{p(1)}\vert U(\xi_1,\xi_2)\vert\nu_{p'(1)}\nu_{p'(2)}...\nu_{p'(N)}\rangle$$

$$= \frac{1}{N!}\sum_{pp'} \langle \nu_{p(N)}...\nu_{p(3)}\vert\nu_{p... ...gle\nu_{p(2)}\nu_{p(1)}\vert U(\xi_1,\xi_2)\vert\nu_{p'(1)}\nu_{p'(2)}\rangle .$$

Again, only those terms survive where $\nu_{p(N)}=\nu_{p'(N)}$,..., $\nu_{p(3)}=\nu_{p'(3)}$. We could have, e.g., $p(1)=4$ and $p(2)=7$ in which case neither $4$ nor $7$ can't be among the $p'(3)$,..., $p'(N)$ (this would yield zero overlap in $\langle \nu_{p(N)}...\nu_{p(3)}\vert\nu_{p'(3)}...\nu_{p'(N)}\rangle$) and therefore $4$ and $7$ must be among ${p'(1)}$ and ${p'(2)}$.

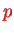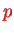This means we get two possibilities for the permutation pairs $p$ and $p'$ now: one with $\nu_{p(1)}=\nu_{p'(1)}$ and $\nu_{p(2)}=\nu_{p'(2)}$, and the other with $\nu_{p(1)}=\nu_{p'(2)}$ and $\nu_{p(2)}=\nu_{p'(1)}$. In the first case $\nu_{p(1)}=\nu_{p'(1)}$, $\nu_{p(2)}=\nu_{p'(2)}$, $\nu_{p(3)}=\nu_{p'(3)}$,..., $\nu_{p(N)}=\nu_{p'(N)}$ which means the permutaton $p'$ is the same as $p$. 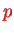In the second case, $p'$ is the same permutation as $p$ apart from one additional swap of $p(1)$ and $p(2)$: this means that ${\rm sign}(p')= - {\rm sign}(p)$ and therefore

$$\langle \Psi \vert U(\xi_1,\xi_2)\vert \Psi\rangle= \frac{1}{N!}\... ...ngle\nu_{p(1)}\nu_{p(2)}\vert U(\xi_1,\xi_2) \vert\nu_{p(1)}\nu_{p(2)}\rangle .$$

The sum over all pairs $i,j$ now again yields

$$\langle \Psi \vert\hat{U}\vert \Psi\rangle= \frac{1}{N!}\sum_{p}\... ...le -\langle\nu_{p(i)}\nu_{p(j)}\vert U \vert\nu_{p(i)}\nu_{p(j)}\rangle \right]$$

$$= \frac{1}{2} \sum_{i\ne j}\left[\langle\nu_{j}\nu_{i}\vert U \vert... ...\nu_{j}\rangle -\langle\nu_{i}\nu_{j}\vert U \vert\nu_{i}\nu_{j}\rangle\right].$$ (2.6)