Expectation value of $\hat{\mathcal H}_0$

Let us consider a $N$-Fermion state (Slater determinant), cf. Eq. (III.1.24),

$$\vert\Psi\rangle = \vert\nu_1\nu_2...\nu_N\rangle_A = \frac{1}{\sqrt{N!}}\sum_p \hat{\Pi}_p {\rm sign}(p) \vert\nu_{p(1)}\nu_{p(2)}...\nu_{p(N)}\rangle.$$ (2.2)

We wish to calculate the expectation value $\langle \Psi \vert\hat{\mathcal H}_0\vert \Psi\rangle$ with $\hat{\mathcal H}_0$ from Eq. (IV.2.1). Consider for example the free Hamiltonian $\hat{H}_0^{(1)}$ for the first particle,

$$\langle \Psi \vert\hat{H}_0^{(1)}\vert \Psi\rangle = \frac{1}{N!}\sum_{pp'} {\rm sign}(p){\rm sign}(p') \langle \nu_{p... ...\nu_{p(1)}\vert\hat{H}_0^{(1)} \vert\nu_{p'(1)}\nu_{p'(2)}...\nu_{p'(N)}\rangle$$

$$= \frac{1}{N!}\sum_{pp'} {\rm sign}(p){\rm sign}(p') \langle \nu_{p... ..._{p'(N)}\rangle \langle\nu_{p(1)}\vert\hat{H}_0^{(1)} \vert\nu_{p'(1)}\rangle .$$

For $N-1$ numbers we must have $p(2)=p'(2)$,..., $p(N)=p'(N)$ (otherwise the term is zero), but if you have a permutation with $N-1$ terms fixed, the last term ist automatically fixed and we have $p=p'$, thus (note ${\rm sign}(p)^2=1$)

$$\langle \Psi \vert\hat{H}_0^{(1)}\vert \Psi\rangle = \frac{1}{N!}\sum_{p} \langle\nu_{p(1)}\vert\hat{H}_0^{(1)} \vert\nu_{p(1)}\rangle.$$ (2.3)

The sum of the single-particle Hamiltonians yields

$$\langle \Psi \vert\hat{\mathcal H}_0\vert \Psi\rangle=$$ (2.4)

$$= \frac{1}{N!}\sum_{p} \langle\nu_{p(1)}\vert\hat{H}_0^{(1)}\vert\n... ...2)}\rangle +... + \langle\nu_{p(N)}\vert\hat{H}_0^{(N)} \vert\nu_{p(N)}\rangle,$$

but all the Hamiltonians $\hat{H}_0^{(i)}$ have the same form, the sum $\sum_p$ just gives $N!$ identical terms, and therefore

$$\langle \Psi \vert\hat{\mathcal H}_0\vert \Psi\rangle= \sum_{i=1}^{N}\langle\nu_{i}\vert\hat{H}_0\vert\nu_{i}\rangle,$$ (2.5)

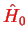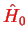where we can omit the index $^{(i)}$ in $\hat{H}_0^{(i)}$ and write $\hat{H}_0$ for the free Hamiltonian of a single particle (note that $\hat{\mathcal H}_0$ in Eq. (IV.2.1) is the total free Hamiltonian; some books use $\hat{h_0}$ instead of $\hat{H}_0$ to make this distinction clearer, but small letters are not nice as a notation for a Hamiltonian).