Discussion of the Born-Oppenheimer Approximation

We now have to justify the neglect of the underlined term in

$$\mathcal{H} \psi_e \phi_n = {\mathcal E} \psi_e\phi_n + \underline{\left[ \mathcal{H}_{\rm n}\psi_e \phi_n - \psi_e\mathcal{H}_{\rm n} \phi_n\right]}.$$ (2.8)

Up to here, everything was still fairly general. Now we make out choice for $\mathcal{H}_{\rm n}$ as just the kinetic energy of the nuclei,

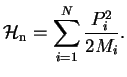$$\mathcal{H}_{\rm n}=\sum_{i=1}^{N} \frac{P_i^2}{2M_i}.$$ (2.9)

We simplify the following discussion by writing

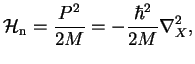$$\mathcal{H}_{\rm n}=\frac{P^2}{2M}=-\frac{\hbar^2}{2M}\nabla_X^2,$$ (2.10)

which refers to a) a single relative motion of two nuclei of effective mass $M$, or alternatively b) represents an `abstract notation' for $\mathcal{H}_{\rm n}=\sum_{i=1}^{N} \frac{P_i^2}{2M_i}$ (to which the following transformations can easily be generalised).

We write

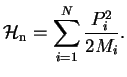
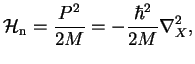
$$\mathcal{H}_{\rm n}\psi_e \phi_n - \psi_e\mathcal{H}_{\rm n} \phi... ... \left[\nabla_X^2 \psi_e(q,X) \phi_n(X) - \psi_e(q,X)\nabla_X^2\phi_n(X)\right]$$

$$= -\frac{\hbar^2}{2M} \Big[ \nabla_X \left\{\phi_n \nabla_X\psi_e + \phi_e \nabla_X\psi_n \right\} -\psi_e\nabla_X^2\phi_n\Big]$$

$$= -\frac{\hbar^2}{2M} \Big[ 2 \nabla_X\phi_n \nabla_X\psi_e + \phi_n \nabla_X^2 \psi_e\Big].$$ (2.11)

This term is therefore determined by the derivative of the electronic part with respect to the nuclear positions $X$, and it has the factor $1/M$ in front. The `handwaving' argument now is to say that the derivatives $\nabla_X\psi_e$ and $\nabla_X^2\psi_e$ are small.