




Next: Discussion of the Born-Oppenheimer
Up: Derivation
Previous: Unsuccessful Attempt
Contents
Index
As
 depends on the positions of the nuclei
depends on the positions of the nuclei
 , let us try an ansatz
, let us try an ansatz
where now the electronic part depends on the nuclear coordinates
 as well. This looks unsymmetric: why shouldn't one have
as well. This looks unsymmetric: why shouldn't one have
 ? First, there is an asymmetry in the problem in the form of
? First, there is an asymmetry in the problem in the form of
 , and
, and
 is no more better than
is no more better than
 in the first place.
in the first place.
The idea with writing
 is that the electronic part
is that the electronic part
 already solves part of the problem, i.e.
already solves part of the problem, i.e.
![$\displaystyle \left[\mathcal{H}_{\rm e}(q,p)+\mathcal{H}_{\rm en}(q,X)\right] \psi_e(q,X)= E(X) \psi_e(q,X),$](img764.png) |
|
|
(2.3) |
an equation in which
 , of course, appears as an external classical parameter that commutes with all other variables. Consequently, the eigenvalue
, of course, appears as an external classical parameter that commutes with all other variables. Consequently, the eigenvalue
 has to depend on
has to depend on
 . We thus obtain
. We thus obtain
where the last questionmark indicated what we would like to have! Since
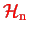 and
and
 depend on the nuclear coordinates only, one would like to use an equation like
depend on the nuclear coordinates only, one would like to use an equation like
![$\displaystyle \left[\mathcal{H}_{\rm n}+ E(X) \right] \phi_n(X) = {\mathcal E} \phi_n(X),$](img769.png) |
|
|
(2.5) |
because then we would have achieved our goal. However, the operator
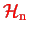 contains the nuclear momenta
contains the nuclear momenta
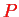 which operate on the
which operate on the
 in
in
 , i.e.
, i.e.
This shows that we are almost there if it wasn't for the underlined term. One now tries to find arguments why this term can be neglected. If it can be neglected, then we have achieved the full solution of the Schrödinger equation by the two separate equations
![$\displaystyle \left[\mathcal{H}_{\rm e}(q,p)+\mathcal{H}_{\rm en}(q,X)\right] \psi_e(q,X)$](img772.png) |
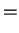 |
 electronic part electronic part |
|
![$\displaystyle \left[\mathcal{H}_{\rm n}+ E(X) \right] \phi_n(X)$](img774.png) |
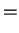 |
 nuclear part nuclear part |
(2.7) |
These two equations Eq. (V.2.7) are the central equations of the Born-Oppenheimer approximation. Even without solving them, some quite interesting observations can already be made:
- The electronic part is calculated as if the nuclei were at fixed positions
 (`clamped nuclei').
(`clamped nuclei').
- The eigenvalue of the energy of the electronic part serves as a potential energy for the nuclei in the nuclear part of the equations.





Next: Discussion of the Born-Oppenheimer
Up: Derivation
Previous: Unsuccessful Attempt
Contents
Index
Tobias Brandes
2005-04-26
![]() is that the electronic part
is that the electronic part
![]() already solves part of the problem, i.e.
already solves part of the problem, i.e.