Rayleigh-Ritz Results

Next: Explicit Calculation of , Up: Bonding and Antibonding Previous: Bonding and Antibonding Contents Index

Rayleigh-Ritz Results

We require the matrices $\bgroup\color{col1}$ \underline{\underline{H}}$\egroup$ and $\bgroup\color{col1}$ \underline{\underline{S}}$\egroup$ ,

$\displaystyle \underline{\underline{H}}$	$\displaystyle =$	$\displaystyle \left(\begin{array}{cc} \alpha & \beta \\ \beta & \alpha \end{ar... ...rline{\underline{S}}=\left(\begin{array}{cc} 1 & S \\ S & 1 \end{array}\right)$	(3.12)
$\displaystyle \alpha$	$\displaystyle \equiv$	$\displaystyle \langle \psi_1 \vert H\vert \psi_1 \rangle = \langle \psi_2 \vert... ...si_1 \vert H\vert \psi_2 \rangle, \quad S = \langle \psi_1 \vert\psi_2 \rangle.$

We have to solve

$\displaystyle {\rm det}\left\vert \underline{\underline{H}} -E \underline{\underline{S}}\right\vert$	$\displaystyle =$	$\begin{displaymath}0 \leadsto {\rm det}\left\vert \begin{array}{cc} \alpha-E & \beta-ES \\ \beta-ES & \alpha-E \end{array}\right\vert=0\end{displaymath}$
	$\displaystyle \leadsto$	$\displaystyle (\alpha-E)^2 - (\beta-ES)^2= 0 \leadsto \alpha-E = \pm (\beta-ES)$
$\displaystyle E_+$	$\displaystyle =$	$\displaystyle \frac{\alpha+\beta}{1+S},\quad E_- = \frac{\alpha-\beta}{1-S}.$	(3.13)

This give the eigenvalues of the energy, $\bgroup\color{col1}$ E_{\pm}$\egroup$ . We find the eigenvectors $\bgroup\color{col1}$ (x_1,x_2)$\egroup$ from

		$\displaystyle (\alpha-E_{\pm} ) x_1 + (\beta-E_{\pm} S) x_2 =0$	(3.14)
$\displaystyle E_+$	$\displaystyle :$	$\displaystyle ((1+S)\alpha -(\alpha+\beta)) x_1 + ((1+S)\beta - (\alpha+\beta)S) x_2 =0$
		$\displaystyle (S\alpha-\beta) x_1 + (\beta -S\alpha)x_2=0\leadsto x_1=x_2\equiv x_+ .$
$\displaystyle E_-$	$\displaystyle :$	$\displaystyle ((1-S)\alpha -(\alpha-\beta)) x_1 + ((1-S)\beta - (\alpha-\beta)S) x_2 =0$
		$\displaystyle (-S\alpha+\beta) x_1 + (\beta -S\alpha)x_2=0\leadsto x_1=-x_2\equiv x_-.$	(3.15)

The normalisation constant is determined from

$\displaystyle 1$	$\displaystyle =$	$\displaystyle \langle \Psi \vert \Psi \rangle = x_1^2 + x_2^2 + 2 x_1x_2 \langle \psi_1 \vert\psi_2 \rangle = x_1^2 + x_2^2 + 2 x_1x_2S$
$\displaystyle \leadsto 1$	$\displaystyle =$	$\displaystyle x_+^2 + x_+^2 + 2 x_+^2 S \leadsto \underline{x_+=\frac{1}{\sqrt{2(1+S)}}}$	(3.16)
$\displaystyle \leadsto 1$	$\displaystyle =$	$\displaystyle x_-^2 + x_-^2 - 2 x_-^2 S \leadsto \underline{x_-=\frac{1}{\sqrt{2(1-S)}}}.$	(3.17)

Summarising, we therefore have obtained the two molecular orbitals (MOs) with energies $\bgroup\color{col1}$ E_{\pm}$\egroup$ ,

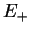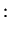$\displaystyle E_+$	$\displaystyle :$	$\displaystyle \Psi_+ = \frac{1}{\sqrt{2(1+S)}} \left( \psi_1 + \psi_2\right)$ bonding	(3.18)
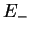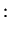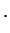$\displaystyle E_-$	$\displaystyle :$	$\displaystyle \Psi_- = \frac{1}{\sqrt{2(1-S)}} \left( \psi_1 - \psi_2\right)$ antibonding $\displaystyle .$	(3.19)

Note that the normalisation factor is different for the two MOs, this is due to the fact that the original AOs (atomic orbitals) are not orthogonal.

Next: Explicit Calculation of , Up: Bonding and Antibonding Previous: Bonding and Antibonding Contents Index

Tobias Brandes 2005-04-26