Explicit Calculation of $\alpha$, $\beta$, $S$

This is required in order to find the values for the two energies $E_{\pm}$, and also in order to find out which of the two states $\Psi_{\pm}$ has lower energy! The calculations are performed by introducing elliptical coordinates $1\le \mu\le \infty$, $-1\le \nu\le 1$, $0\le \phi\le 2\pi$,

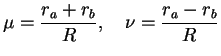$$\mu=\frac{r_a+r_b}{R},\quad \nu=\frac{r_a-r_b}{R}$$ (3.20)

and noting that the volume element in these coordinates is

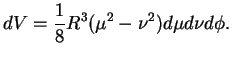$$dV=\frac{1}{8}R^3(\mu^2-\nu^2) d\mu d\nu d\phi.$$ (3.21)

The result for $\alpha$, $\beta$, and $S$ is found as a function of the (fixed) distance $R$ between the two protons. Using this together with Eq. (V.3.13), one finally obtains

$$E_+ = E_{1s}+\frac{e^2}{4\pi\varepsilon_0 a_0}\left[\frac{1}{R}-\frac{j+k}{1+S}\right]$$

$$E_- = E_{1s}+\frac{e^2}{4\pi\varepsilon_0a_0}\left[\frac{1}{R}+\frac{j-k}{1-S}\right]$$

$$R \equiv \vert{\bf r}_a-{\bf r}_b\vert/a_0,\quad S \equiv \left(1+R+\frac{1}{3}R^2\right)e^{-R}$$ (3.22)

$$j \equiv a_0\int dV \frac{\vert\psi_{1s}({\bf r}-{\bf r}_a)\vert^2}{\vert{\bf r}-{\bf r}_b\vert)} = \frac{1}{R}\left(1-(1+R)e^{-2R}\right)$$

$$k \equiv a_0\int dV \frac{\psi_{1s}({\bf r}-{\bf r}_a)\psi_{1s}({\bf r}-{\bf r}_b) }{\vert{\bf r}-{\bf r}_a\vert)}= (1+R)e^{-R} .$$

Be careful because I haven't checked these explicit expressions, which are from Atkins/Friedman [5] ch. 8.3.

Figure: Energy level splitting for $\Psi_+$ (a) and $\Psi_-$ (b), from Weissbluth [4].

REMARKS:

• The energies $j$ and $k$ are here written as dimensionless quantities.
• The energy $j$ is due to the electron charge density around nucleus $a$ in the Coulomb field of nucleus $b$. The energy $k$ is an interference term.
• One has $j>k$ and therefore the energy $E_+$ corresponding to the bonding state is the lower of the two: Occupation of the bonding orbital $\Psi_+$ lowers the energy of the molecule and `draws the two nuclei together', as we will see from the curve $E_+(R)$ below which represents the potential in BO approximation for the two nuclei. The bonding orbital corresponds to a wave function with even parity with respect to with respect to reflections at the plane that lies symmetrically between the two nuclei.
• The antibonding orbital $\Psi_-$ has a larger energy. It corresponds to an odd wave function.
• For the Hydrogen ion, sometimes one uses the notation (cf. Weissbluth [4] ch. 26.2)
  

  $$\Psi_+ \equiv 1\sigma_{\rm g}^+$$ (3.23)

  $$\Psi_- \equiv 1\sigma_{\rm u}^+ ,$$ (3.24)

  
  
  where the indices mean even for $g$ (German `gerade') and odd for $u$ (German `ungerade') and $\sigma^+$ referring to a symmetry (see below).

The charge distribution in $\Psi_+$ and $\Psi_-$ is shown in Fig.(V.3.3.2).

Figure: Charge distribution in $\Psi_+$ (a) and $\Psi_-$ (b), from Weissbluth [4].