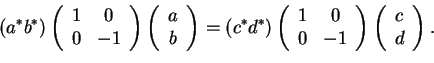Next: Axioms of Quantum Mechanics
Previous: ** Determinant of (10
Contents
We consider a one-dimensional potential of the form
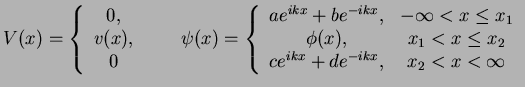 |
(21) |
Here, 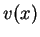 is an arbitrary real potential. The central part
is an arbitrary real potential. The central part 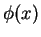 of the wave function
of the wave function 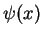 therefore in general is very difficult to calculate. We can, however, relate the coefficients
therefore in general is very difficult to calculate. We can, however, relate the coefficients
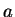 ,
, 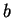 (left side) with the coefficients
(left side) with the coefficients 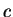 ,
, 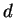 (right side): if some fixed values for
(right side): if some fixed values for 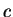 and
and 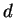 are
chosen, this determines the solution
are
chosen, this determines the solution 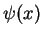 everywhere on the
everywhere on the 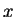 -axis and therefore in particular
-axis and therefore in particular
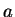 and
and 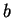 . We write this relation as
. We write this relation as
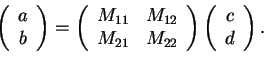 |
|
|
(22) |
a) With 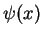 also the conjugate complex
also the conjugate complex 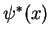 must be a solution of the
stationary Schrödinger equation
must be a solution of the
stationary Schrödinger equation
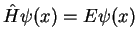 . Why ?
. Why ?
b) Take the conjugate complex 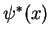 in
(2.21) and show that this
leads to the exchange
in
(2.21) and show that this
leads to the exchange
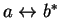 and
and
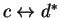 in (2.22).
in (2.22).
c) Take the conjugate complex of the whole equation
(2.22) and compare with the equation you obtain from
part b). Show that
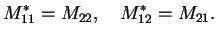 |
|
|
(23) |
d) Consider the current density and show that
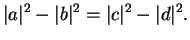 |
|
|
(24) |
Write this equation as a scalar product of vectors in the form
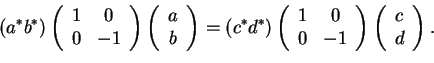 |
|
|
(25) |
Use the matrix 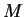 to derive from this
to derive from this
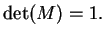 |
|
|
(26) |




Next: Axioms of Quantum Mechanics
Previous: ** Determinant of (10
Contents
Tobias Brandes
2004-02-04
![]() in
(2.21) and show that this
leads to the exchange
in
(2.21) and show that this
leads to the exchange
![]() and
and
![]() in (2.22).
in (2.22).