



Next: About this document ...
Up: The Angular Momentum
Previous: The Angular Momentum
Contents
In classical mechanics, the angular momentum of an object with position 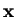 and
momentum
and
momentum 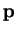 is defined as
is defined as
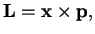 |
|
|
(295) |
that is the cross product (vector product) of the position and the momentum. In components, this is
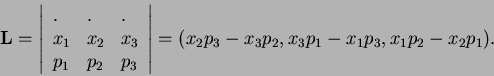 |
|
|
(296) |
The corresponding quantum mechanical operator is obtained from the correspondence principle
that replaces
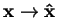 , i.e. the position operator, and
, i.e. the position operator, and
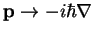 , i.e. the momentum operator. Because we are in three dimensions,
the operators are vectors:
, i.e. the momentum operator. Because we are in three dimensions,
the operators are vectors:
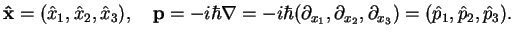 |
|
|
(297) |
The angular momentum operator therefore becomes
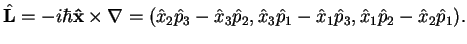 |
|
|
(298) |
In polar coordinates, one has to use the spherical polar expression for the Nabla
operator that you learned in vector analysis. The corresponding expression for
the components of the angular momentum operator become
Notice that in spherical polar coordinates, the 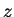 -axis is the central axis of the coordinate system with the
angle
-axis is the central axis of the coordinate system with the
angle 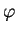 revolving around it. The angular momentum
revolving around it. The angular momentum 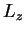 corresponds to revolutions around the
corresponds to revolutions around the 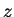 -axis,
its quantum mechanical expression becomes quite simple: basically, just a differentiation with respect
to the angle
-axis,
its quantum mechanical expression becomes quite simple: basically, just a differentiation with respect
to the angle 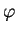 `around the
`around the 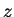 axis'.
axis'.
Another important observation is that the angular momentum square, that is the operator
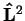 , becomes
, becomes
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...a}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right].$](img1264.png) |
|
|
(300) |
We notice that this is just 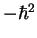 times the expression
times the expression
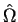 , eq. (4.61), for the
angular part of the Laplacian
, eq. (4.61), for the
angular part of the Laplacian 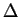 ! In particular, the eigenfunctions
! In particular, the eigenfunctions 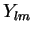 of
of
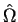 are the eigenfunctions of the angular momentum square, cf. eq.(4.63) with
are the eigenfunctions of the angular momentum square, cf. eq.(4.63) with 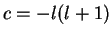 ,
,
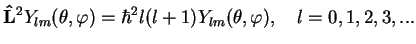 |
|
|
(301) |
Furthermore, the dependence of
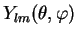 on the angle
on the angle 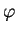 is only through the exponential
is only through the exponential
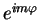 . We thus have
. We thus have
which means that
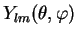 are eigenfunctions of the
are eigenfunctions of the 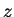 -component of the angular momentum, too.
-component of the angular momentum, too.
The eigenfunctions
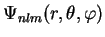 of the Hamiltonian
of the Hamiltonian 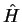 for the hydrogen atom therefore
are also eigenfunctions of
for the hydrogen atom therefore
are also eigenfunctions of
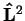 and
and 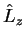 . We summarize this in three equations
. We summarize this in three equations




Next: About this document ...
Up: The Angular Momentum
Previous: The Angular Momentum
Contents
Tobias Brandes
2004-02-04
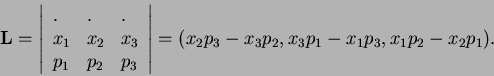
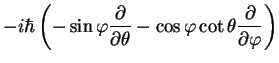
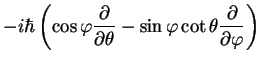
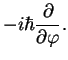
![]() , becomes
, becomes
![$\displaystyle {\bf\hat{L}}^2=
-\hbar^2 \left[\frac{1}{\sin \theta}\frac{\partia...
...a}\right)
+\frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}\right].$](img1264.png)
![]() of the Hamiltonian
of the Hamiltonian ![]() for the hydrogen atom therefore
are also eigenfunctions of
for the hydrogen atom therefore
are also eigenfunctions of
![]() and
and ![]() . We summarize this in three equations
. We summarize this in three equations