



Next: Math Revision: Eigenvalues of
Up: The Stationary Schrödinger Equation
Previous: The Stationary Schrödinger Equation
Contents
The Schrödinger equation is a partial differential equation: we have one partial derivative
with respect of time 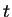 and the Laplace operator
and the Laplace operator 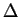 which is a differential operator,
which is a differential operator,
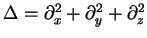 in three dimensions and rectangular coordinates.
in three dimensions and rectangular coordinates.
Step 1: To solve (2.1), we make the separation ansatz
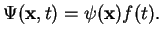 |
|
|
(79) |
Inserting into (2.1) we have
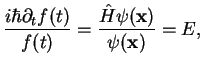 |
|
|
(80) |
where we have separated the 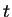 - and the
- and the 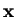 -dependence. Both sides of (2.3)
depend on
-dependence. Both sides of (2.3)
depend on 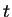 resp.
resp. 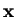 independently and therefore must be constant
independently and therefore must be constant 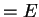 . Solving the
equation for
. Solving the
equation for 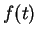 yields
yields
![$ f(t)= \exp[{-iEt/\hbar}]$](img321.png) and therefore
and therefore
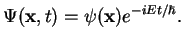 |
|
|
(81) |
We recognize: the time evolution of the wave function
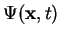 is solely determined by the
factor
is solely determined by the
factor
![$ \exp[{-iEt/\hbar}]$](img323.png) . Furthermore, the constant
. Furthermore, the constant  must be an energy (dimension!).
must be an energy (dimension!).
Step 2: To determine
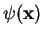 , we have to solve the stationary Schrödinger equation
, we have to solve the stationary Schrödinger equation
![$\displaystyle {\hat{H}\psi({\bf x}) = E \psi({\bf x})} \longleftrightarrow
\left[-\frac{\hbar^2\Delta}{2m} + V({\bf x}) \right]\psi({\bf x})=E\psi({\bf x}).$](img326.png) |
|
|
(82) |
Mathematically, the equation
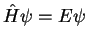 with the operator
with the operator 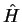 is an eigenvalue equation. We know eigenvalue equations from linear algebra where
is an eigenvalue equation. We know eigenvalue equations from linear algebra where 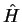 is a
matrix and
is a
matrix and 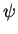 is a vector.
The time-independent wave functions
is a vector.
The time-independent wave functions
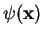 are called stationary wave functions
or stationary states. We will see in the following that in general, solutions of
the stationary Schrödinger equation do not exist for arbitrary
are called stationary wave functions
or stationary states. We will see in the following that in general, solutions of
the stationary Schrödinger equation do not exist for arbitrary  . Rather, many potentials
. Rather, many potentials
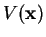 give rise to solutions only for certain discrete values of
give rise to solutions only for certain discrete values of  , the eigenvalues
of the stationary Schrödinger equation, and the possible energy values become quantized.
, the eigenvalues
of the stationary Schrödinger equation, and the possible energy values become quantized.




Next: Math Revision: Eigenvalues of
Up: The Stationary Schrödinger Equation
Previous: The Stationary Schrödinger Equation
Contents
Tobias Brandes
2004-02-04
![]() , we have to solve the stationary Schrödinger equation
, we have to solve the stationary Schrödinger equation