



Next: Stationary states
Up: Wave Mechanics
Previous: Wave Mechanics
Contents
Much of what we will be concerned with in this lecture
are the solutions of the Schrödinger equation for a particle of mass 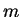 in a potential
in a potential
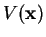 ,
,
![$\displaystyle i\hbar\frac{\partial}{\partial t} \Psi({\bf x},t)
=\left[-\frac{\...
...^2\Delta}{2m} + V({\bf x}) \right]\Psi({\bf x},t)\equiv \hat{H}\Psi({\bf x},t).$](img314.png) |
|
|
(78) |
Like Newton's laws in classical mechanics,
the Schrödinger equation is so important that
generation of physicists have worked out how to solve it for
physically interesting cases. Unfortunately, in general (i.e.
for a general form of the potential
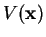 ) the
Schrödinger equation is not exactly soluble, and one has to retreat to
approximate methods. There are, however, important classes of solutions
that can be obtained exactly, most of which were `milestones' in the development
of the theory. Among them are the hydrogen atom, the harmonic oscillator,
or one-dimensional problems which we will discuss in this chapter.
) the
Schrödinger equation is not exactly soluble, and one has to retreat to
approximate methods. There are, however, important classes of solutions
that can be obtained exactly, most of which were `milestones' in the development
of the theory. Among them are the hydrogen atom, the harmonic oscillator,
or one-dimensional problems which we will discuss in this chapter.
Subsections
Tobias Brandes
2004-02-04
![$\displaystyle i\hbar\frac{\partial}{\partial t} \Psi({\bf x},t)
=\left[-\frac{\...
...^2\Delta}{2m} + V({\bf x}) \right]\Psi({\bf x},t)\equiv \hat{H}\Psi({\bf x},t).$](img314.png)