



Next: Piecewise Constant one-Dimensional Potentials
Up: The Stationary Schrödinger Equation
Previous: Math Revision: Eigenvalues of
Contents
In this section, we study the stationary Schrödinger
equation for an important class of potentials
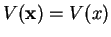 that only depend on one
spatial coordinate
that only depend on one
spatial coordinate 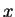 and are independent of
and are independent of 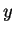 and
and 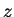 . Such potentials could be generated, for example,
by electric fields that only vary in one direction
. Such potentials could be generated, for example,
by electric fields that only vary in one direction 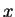 of space and are constant in the other directions.
of space and are constant in the other directions.
We make a separation ansatz for
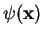 ,
,
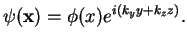 |
|
|
(85) |
Inserting into the stationary Schrödinger equation yields
The general solution therefore can be written as the product of two plane waves running
in the 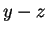 -plane, and a wave function
-plane, and a wave function 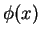 which is
the solution of (2.9). This means we have just to solve
the one-dimensional stationary Schrödinger equation, with the energy
which is
the solution of (2.9). This means we have just to solve
the one-dimensional stationary Schrödinger equation, with the energy  replaced by
replaced by
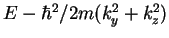 which is the energy for the one-dimensional motion in
the
which is the energy for the one-dimensional motion in
the 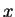 -direction. Together with
-direction. Together with
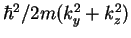 , the kinetic energy of the
motion in the
, the kinetic energy of the
motion in the 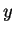 -
-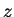 -plane, this is just the total energy
-plane, this is just the total energy  .
With the potential
.
With the potential
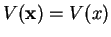 , the particle sees no potential change
when moving in only
, the particle sees no potential change
when moving in only 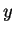 - or
- or 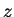 -direction: there is no force acting on the
particle in this direction which is why its free motion turns out to be described by plane
waves in the
-direction: there is no force acting on the
particle in this direction which is why its free motion turns out to be described by plane
waves in the 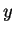 - and
- and 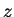 -direction.
-direction.
In the following, we will therefore only consider the rest of the problem, i.e. the motion in
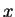 -direction.
-direction.




Next: Piecewise Constant one-Dimensional Potentials
Up: The Stationary Schrödinger Equation
Previous: Math Revision: Eigenvalues of
Contents
Tobias Brandes
2004-02-04
![]() ,
,
![]() -direction.
-direction.