



Next: The Infinite Potential Well
Up: The Stationary Schrödinger Equation
Previous: Stationary States in One
Contents
We consider the one-dimensional stationary Schrödinger equation
where for the sake of a nicer notation we again write  instead of
instead of 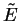 and
and
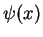 instead of
instead of 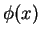 . Furthermore, there is only one variable
. Furthermore, there is only one variable 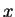 so that the partial derivative
so that the partial derivative
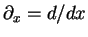 .
.
In the following, we will concentrate on the important case where 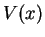 is piecewise constant,
i.e.
is piecewise constant,
i.e.
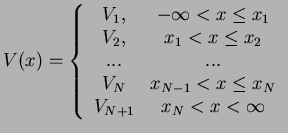 |
(88) |
Let us look at (2.10) on an interval where 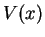 is constant, say
is constant, say ![$ [x_1,x_2]$](img359.png) with
with 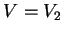 . The Schrödinger equation
. The Schrödinger equation
on this interval is a second order ordinary differential equation with constant coefficients.
There are two independent solutions
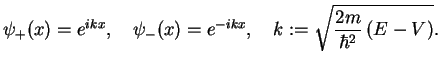 |
|
|
(90) |
1. If 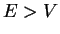 , the wave vector
, the wave vector  is a real quantity and the two solutions
is a real quantity and the two solutions
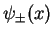 are plane waves running in the positive and the negative
are plane waves running in the positive and the negative 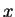 -direction.
Such solutions are called oscillatory solutions.
-direction.
Such solutions are called oscillatory solutions.
2. If 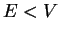 ,
,  becomes imaginary and we write
becomes imaginary and we write
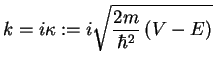 |
|
|
(91) |
with the real quantity 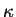 . The two independent solutions then become
exponential functions
. The two independent solutions then become
exponential functions
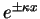 . Such solutions are called exponential solutions.
. Such solutions are called exponential solutions.
For fixed energy  , the general solution
, the general solution 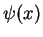 will be a superposition, that is a linear
combination
will be a superposition, that is a linear
combination
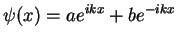 |
|
|
(92) |
with  either real or imaginary,
either real or imaginary, 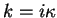 .
Since the wave function in general is a complex function, the coefficients
.
Since the wave function in general is a complex function, the coefficients 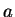 ,
, 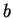 can be complex numbers.
Note that we can not have linear combinations
with one real and one imaginary term in the exponential like
can be complex numbers.
Note that we can not have linear combinations
with one real and one imaginary term in the exponential like
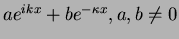 .
.
The solution of our Schrödinger equation with the piece-wise constant potential
(2.11) must fulfill it everywhere on the 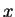 -axis. Therefore, it
can be written as
-axis. Therefore, it
can be written as
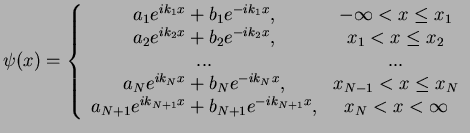 |
(93) |
with complex constants 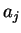 ,
, 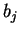 and
and
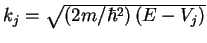 either real or complex.
either real or complex.




Next: The Infinite Potential Well
Up: The Stationary Schrödinger Equation
Previous: Stationary States in One
Contents
Tobias Brandes
2004-02-04
![$\displaystyle \left[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}
+ V({x}) \right]\psi(x)$](img353.png)
![]() is piecewise constant,
i.e.
is piecewise constant,
i.e.
![]() ,
, ![]() becomes imaginary and we write
becomes imaginary and we write
![]() , the general solution
, the general solution ![]() will be a superposition, that is a linear
combination
will be a superposition, that is a linear
combination
![]() -axis. Therefore, it
can be written as
-axis. Therefore, it
can be written as