



Next: The Tunnel Barrier: Transmission
Up: The Tunnel Effect and
Previous: The Tunnel Effect and
Contents
We consider a potential step at 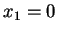 with
with 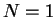 ,
, 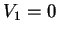 and
and 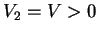 in
(2.42).
in
(2.42).
a) For 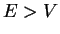 , we have
, we have
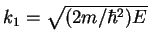 and
and
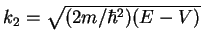 such that from the transfer matrix
such that from the transfer matrix 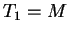 , Eq. (2.46), we obtain
, Eq. (2.46), we obtain
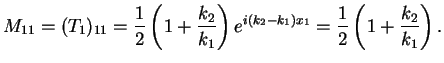 |
|
|
(136) |
This yields the transmission and reflection coefficients
and we recognize that
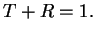 |
|
|
(138) |
Compare this result to the case of a classical particle running
from the bottom to the top of a (soft) step: if its energy  is sufficient
is sufficient 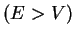 ,
it overcomes the barrier and continues to run on the top of the step, if
its energy is too small, is rolls back and is reflected. In quantum mechanics,
for
,
it overcomes the barrier and continues to run on the top of the step, if
its energy is too small, is rolls back and is reflected. In quantum mechanics,
for 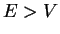 there is a finite probability for the particle being reflected!
there is a finite probability for the particle being reflected!
b) For 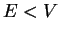 we see that
we see that 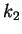 becomes imaginary and there are no longer running waves for
becomes imaginary and there are no longer running waves for 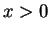 :
the particle then is in the classically forbidden zone. With
:
the particle then is in the classically forbidden zone. With
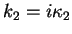 ,
,
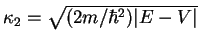 , the wave function on the right is
, the wave function on the right is
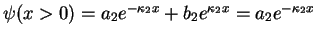 because we had set
because we had set 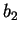 anyway. We therefore can still
apply our scattering formalism to obtain the reflection coefficient
anyway. We therefore can still
apply our scattering formalism to obtain the reflection coefficient
On the right side  , we don't have running waves any longer for
, we don't have running waves any longer for 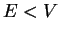 and therefore cannot
apply (2.55) for the transmission coefficient. The particle current density (2.51)
and therefore cannot
apply (2.55) for the transmission coefficient. The particle current density (2.51)
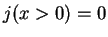 , however, which means
, however, which means 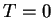 . Again, we have
. Again, we have 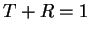 .
.
Compare this case to total reflection of waves in optics!




Next: The Tunnel Barrier: Transmission
Up: The Tunnel Effect and
Previous: The Tunnel Effect and
Contents
Tobias Brandes
2004-02-04
![]() , we have
, we have
![]() and
and
![]() such that from the transfer matrix
such that from the transfer matrix ![]() , Eq. (2.46), we obtain
, Eq. (2.46), we obtain
![]() we see that
we see that ![]() becomes imaginary and there are no longer running waves for
becomes imaginary and there are no longer running waves for ![]() :
the particle then is in the classically forbidden zone. With
:
the particle then is in the classically forbidden zone. With
![]() ,
,
![]() , the wave function on the right is
, the wave function on the right is
![]() because we had set
because we had set ![]() anyway. We therefore can still
apply our scattering formalism to obtain the reflection coefficient
anyway. We therefore can still
apply our scattering formalism to obtain the reflection coefficient