



Next: A more complicated case
Up: The Tunnel Effect and
Previous: The Tunnel Barrier: Transmission
Contents
For energies of the particle 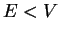 , we have a finite transmission coefficient
, we have a finite transmission coefficient 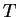 that increases with
that increases with  .
In particular, the wave function below the barrier, i.e. in the interval
.
In particular, the wave function below the barrier, i.e. in the interval ![$ [-a,a]$](img616.png) , is non zero which means
that there is a finite probability to find the particle below the barrier.
This is a very important quantum mechanical phenomenon called the tunnel effect.
Classically, a particle
can not be in areas where the potential energy
, is non zero which means
that there is a finite probability to find the particle below the barrier.
This is a very important quantum mechanical phenomenon called the tunnel effect.
Classically, a particle
can not be in areas where the potential energy 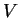 is larger than its total energy
is larger than its total energy  .
.
For energies of the particle 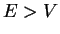 , the transmission coefficient oscillated as a function of energy
, the transmission coefficient oscillated as a function of energy  .
At particular values of
.
At particular values of  , the
, the
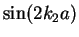 in (2.67)
vanishes, and
in (2.67)
vanishes, and 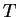 exactly becomes unity. These peaks in
exactly becomes unity. These peaks in 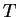 are called transmission resonances.
The condition for the resonance energies is
are called transmission resonances.
The condition for the resonance energies is
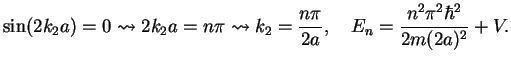 |
|
|
(146) |
We recognize that the energies 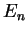 are just the energy eigenvalues of the infinite potential
well of width
are just the energy eigenvalues of the infinite potential
well of width 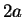 , shifted by the height
, shifted by the height 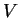 of the potential!
of the potential!




Next: A more complicated case
Up: The Tunnel Effect and
Previous: The Tunnel Barrier: Transmission
Contents
Tobias Brandes
2004-02-04
![]() , the transmission coefficient oscillated as a function of energy
, the transmission coefficient oscillated as a function of energy ![]() .
At particular values of
.
At particular values of ![]() , the
, the
![]() in (2.67)
vanishes, and
in (2.67)
vanishes, and ![]() exactly becomes unity. These peaks in
exactly becomes unity. These peaks in ![]() are called transmission resonances.
The condition for the resonance energies is
are called transmission resonances.
The condition for the resonance energies is