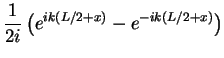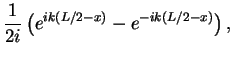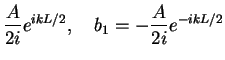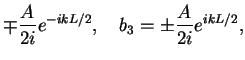Next: Case of no potential
Up: Wave Mechanics
Previous: The tunnel barrier: Discussion
Contents
A more complicated case
We consider a particle of mass 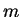 confined in a one-dimensional potential well with infinitely high
walls at
confined in a one-dimensional potential well with infinitely high
walls at 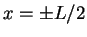 . Within the well, i.e. within the interval
. Within the well, i.e. within the interval
![$ [-a/2,a/2]$](img620.png) ,
, 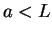 , there is a symmetric
potential
, there is a symmetric
potential
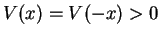 , see Fig. 2.3.
, see Fig. 2.3.
Figure:
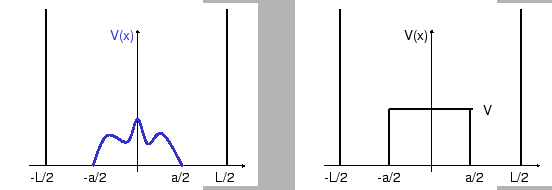
Left: Symmetric potential 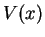 within a one-dimensional potential well.
Right: special case of a rectangular potential.
within a one-dimensional potential well.
Right: special case of a rectangular potential.
 |
We wish to determine the stationary bound states with energy  and the possible energy eigenvalues
and the possible energy eigenvalues
 for this potential.
Because the potential is symmetric around the origin, the eigenstate wave functions must have even or odd parity
for this potential.
Because the potential is symmetric around the origin, the eigenstate wave functions must have even or odd parity
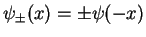 . For
. For 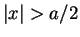 , the wave function must be a superposition
of plane waves that has to vanish at the boundaries
, the wave function must be a superposition
of plane waves that has to vanish at the boundaries 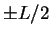 . Therefore, we can set
. Therefore, we can set
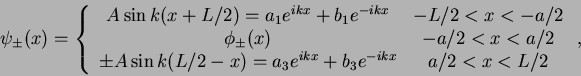 |
|
|
(147) |
where 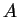 is a complex constant,
is a complex constant,
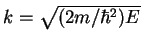 and
and
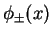 the wave function
within the potential region
the wave function
within the potential region 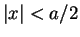 .
It is convenient to write the even (
.
It is convenient to write the even (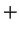 ) and odd (
) and odd (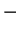 ) wave functions within one line, using the definitions
) wave functions within one line, using the definitions
Here, 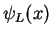 is localized only in the left part
is localized only in the left part 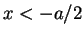 and
and
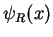 is localized only in the right part
is localized only in the right part 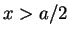 of the well.
of the well.
We now use our transfer matrix formalism to obtain the equation that determines the possible energy values  :
The solution on the left of the potential
:
The solution on the left of the potential 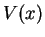 is connected to the solution on the right, cf.
eq. (2.54),
is connected to the solution on the right, cf.
eq. (2.54),
Using
we identify
which yields two linear equations
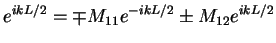 |
|
|
|
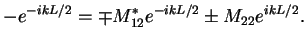 |
|
|
(151) |
Here, the upper sign always holds for the even solution 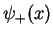 while the lower sign holds
for the odd solution
while the lower sign holds
for the odd solution 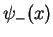 . In fact, for a symmetric potential
. In fact, for a symmetric potential
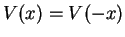 ,
,
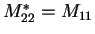 and
and
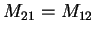 such that the second of the above equations
is just the conjugate complex of the first.
The condition that determines the possible wave vectors
such that the second of the above equations
is just the conjugate complex of the first.
The condition that determines the possible wave vectors  and therewith the energies
and therewith the energies
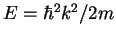 is
is
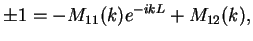 |
|
|
(152) |
where we explicitly indicated the  -dependence of the transfer matrix elements.
-dependence of the transfer matrix elements.
Subsections




Next: Case of no potential
Up: Wave Mechanics
Previous: The tunnel barrier: Discussion
Contents
Tobias Brandes
2004-02-04
![]() confined in a one-dimensional potential well with infinitely high
walls at
confined in a one-dimensional potential well with infinitely high
walls at ![]() . Within the well, i.e. within the interval
. Within the well, i.e. within the interval
![]() ,
, ![]() , there is a symmetric
potential
, there is a symmetric
potential
![]() , see Fig. 2.3.
, see Fig. 2.3.

![]() :
The solution on the left of the potential
:
The solution on the left of the potential ![]() is connected to the solution on the right, cf.
eq. (2.54),
is connected to the solution on the right, cf.
eq. (2.54),