




Next: Solution of the PDE
Up: -representation
Previous: Derivation of the PDE
Contents
Index
In this case, we only have first order derivatives. There is a (more or less) complete theory of first order PDEs: they are solved by the method of characteristics (cf. Courant/Hilbert).
We write the PDE as
![$\displaystyle \left\{ \frac{\partial}{\partial t}
- i\left[ \bar{\Omega} - i\ka...
...a\right]z^*\frac{\partial}{\partial z^*}
\right\} P(z,z^*t) = 2\kappa P(z,z^*t)$](img347.png) |
|
|
(80) |
and consider the function
 on trajectories
on trajectories  and
and
 where
where
 . We regard the l.h.s. of Eq.(7.81) as a total differential.
Along the trajectories, the
temporal change of
. We regard the l.h.s. of Eq.(7.81) as a total differential.
Along the trajectories, the
temporal change of 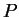 is
is
Comparison yields
On the other hand,
 yields
yields
Here,  is the initial condition for
is the initial condition for 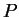 , with
, with
 and
and
 . This looks very innocent but has a deep physical
(and geometrical) meaning: we can trace back our trajectories
. This looks very innocent but has a deep physical
(and geometrical) meaning: we can trace back our trajectories
 ,
, to their origin
to their origin  ,
,  , writing
, writing
We thus have expressed the inital values  ,
,  in terms
of the `final' values
in terms
of the `final' values  ,
, . Insertion into Eq.(7.84)
yields
. Insertion into Eq.(7.84)
yields
We now write again  and
and  instead of
instead of  ,
,  , and
therefore have
, and
therefore have





Next: Solution of the PDE
Up: -representation
Previous: Derivation of the PDE
Contents
Index
Tobias Brandes
2004-02-18

![$\displaystyle - i\left[ \bar{\Omega} - i\kappa\right]z(t)\leadsto
z(t)=z_0e^{- i\left[ \bar{\Omega} - i\kappa\right]t}$](img356.png)
![$\displaystyle i\left[ \bar{\Omega} + i\kappa\right]z^*(t)\leadsto
z^*(t)=z_0^*e^{ i\left[ \bar{\Omega} + i\kappa\right]t}.$](img358.png)
![$\displaystyle z(t)e^{+i\left[ \bar{\Omega} - i\kappa\right]t},\quad
z_0^*= z^*(t)e^{-i\left[ \bar{\Omega} + i\kappa\right]t}.$](img370.png)
![$\displaystyle e^{2\kappa t}P_0\left(
z(t)e^{+i\left[ \bar{\Omega} - i\kappa\right]t},
z^*(t)e^{-i\left[ \bar{\Omega} + i\kappa\right]t}\right).$](img371.png)
![$\displaystyle e^{2\kappa t}P_0\left(
ze^{+i\left[ \bar{\Omega} - i\kappa\right]t},
z^*e^{-i\left[ \bar{\Omega} + i\kappa\right]t}\right).$](img373.png)