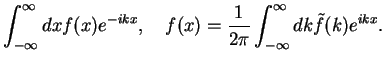 |
(43) |
1. In this lecture, we define the Fourier transform with the
factor ![]() as in (1.43). Some people define it symmetrically, i.e.
as in (1.43). Some people define it symmetrically, i.e.
![]() in front of
in front of ![]() and
and
![]() .
.
2. Remember the Minus signs in the ![]() functions.
functions.
We often use the Fourier transform
![]() in
in ![]() dimensions for a function
dimensions for a function
![]() ,
,
![]() ,
,