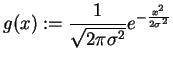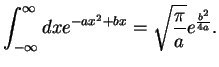Next: The Delta Functional (`Delta
Up: Fourier Transforms and the
Previous: Math: Fourier Integral
Contents
The Gauss function
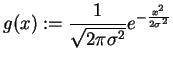 |
|
|
(45) |
is a convenient example to discuss properties of the Fourier transform.
It can be decomposed into plane waves by
An important integral in this context is
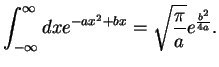 |
|
|
(47) |
A very broad Gauss function 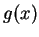 with large
with large 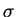 is the result of
a superposition of plane waves
is the result of
a superposition of plane waves 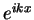 in a very small range of
in a very small range of 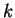 -values around
-values around 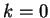 : if
: if
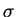 is very large, the weights
is very large, the weights
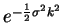 in the Fourier decomposition
become very small for large
in the Fourier decomposition
become very small for large 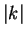 . Discuss the opposite case of small
. Discuss the opposite case of small 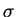 !
!




Next: The Delta Functional (`Delta
Up: Fourier Transforms and the
Previous: Math: Fourier Integral
Contents
Tobias Brandes
2004-02-04