



Next: * Partial Differential Equations
Up: Fourier Transforms and the
Previous: Math: Gauss function
Contents
The parameter 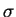 in the Gauss function determines its width. A broad wave packet in coordinate
(
in the Gauss function determines its width. A broad wave packet in coordinate
(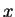 ) space
corresponds to a narrow distribution of wave vectors
) space
corresponds to a narrow distribution of wave vectors  .
What happens in the limit
.
What happens in the limit
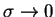 ? In coordinate space, this would correspond to an extremely sharp
wave packet around
? In coordinate space, this would correspond to an extremely sharp
wave packet around 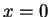 that could serve as a model for a particle localized at
that could serve as a model for a particle localized at 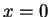 .
We define
.
We define
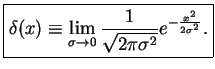 |
|
|
(48) |
As an ordinary function, this is a somewhat strange mathematical object because it is zero for all 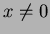 , but
infinite for
, but
infinite for 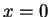 . However, it has the useful property that for any (reasonably well-behaving) function
. However, it has the useful property that for any (reasonably well-behaving) function 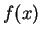
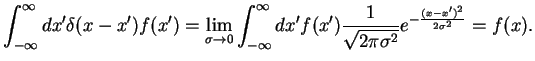 |
|
|
(49) |
For example, multiplication of 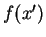 with
with
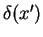 and integration over the whole
and integration over the whole 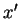 -axis gives the value
of
-axis gives the value
of 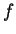 at
at 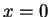 . Such an operation is called a functional, that is a mapping
. Such an operation is called a functional, that is a mapping
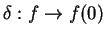 |
|
|
(50) |
that puts a
whole function 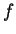 to a (complex or real) number. Nevertheless, for historical reasons physicists call this
object a delta-function. Remember that
to a (complex or real) number. Nevertheless, for historical reasons physicists call this
object a delta-function. Remember that 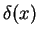 is only defined as in (1.49), that is
by integration over a function (`test-function')
is only defined as in (1.49), that is
by integration over a function (`test-function') 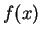 .
.
Another very useful property is the Fourier transform of the Delta-function:
We recall our definition
Now, comparing with the definition of the Delta function, Eq.(1.49), we recognise
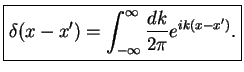 |
|
|
(52) |
The delta function is thus a superposition of all plane waves; the corresponding
distribution of  -values
in
-values
in  -space is `extremely broad', that is uniform from
-space is `extremely broad', that is uniform from 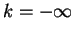 to
to 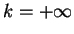 .
Note that we can also obtain the result
.
Note that we can also obtain the result
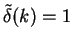 from the Fourier transform
from the Fourier transform
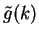 of the Gauss function
of the Gauss function 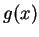 , Eq. (1.46), in the limit
, Eq. (1.46), in the limit
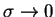 .
.




Next: * Partial Differential Equations
Up: Fourier Transforms and the
Previous: Math: Gauss function
Contents
Tobias Brandes
2004-02-04
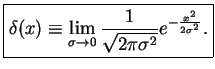
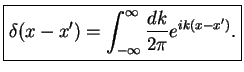
![]() -values
in
-values
in ![]() -space is `extremely broad', that is uniform from
-space is `extremely broad', that is uniform from ![]() to
to ![]() .
Note that we can also obtain the result
.
Note that we can also obtain the result
![]() from the Fourier transform
from the Fourier transform
![]() of the Gauss function
of the Gauss function ![]() , Eq. (1.46), in the limit
, Eq. (1.46), in the limit
![]() .
.