



Next: The Angular Momentum
Up: The Hydrogen Atom
Previous: The Angular Part
Contents
The radial part of the Schrödinger equation is obtained from (4.62) with
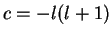 ,
,
![$\displaystyle \frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2
\frac{\partial...
...)}{\partial r}\right)+\frac{2m}{\hbar^2}[E-V(r)]R(r)
-\frac{l(l+1)}{r^2}R(r)=0.$](img1239.png) |
|
|
(290) |
For the hydrogen atom, the attractive Coulomb potential generated by the proton
(charge 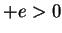 ,
,  ) is
) is
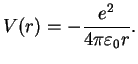 |
|
|
(291) |
Strictly speaking, we are now dealing with a problem where many particles are involved:
the electron and the proton which itself is composed of smaller elementary particles, the
quarks. In such cases our single particle Schrödinger equation is no longer strictly valid.
We neglect the inner structure of the proton and also use the fact that it is much heavier
than the electron. As in the case of other two-body problems one can introduce
center-of-mass and relative coordinates and reduce the problem to a one-particle problem.
The mass 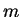 is a reduced mass but it is very close to the electron mass.
is a reduced mass but it is very close to the electron mass.
Again, we do not explicitely solve for the possible energy eigenvalues  and the radial eigenfunctions
here but present the result: For bound states where the electron is bound to the attractive
potential, the possible eigenvalues
and the radial eigenfunctions
here but present the result: For bound states where the electron is bound to the attractive
potential, the possible eigenvalues 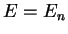 are labeled by a quantum number
are labeled by a quantum number 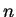 ,
,
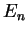 |
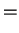 |
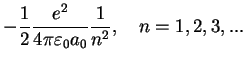 Lyman Formula Lyman Formula |
|
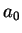 |
 |
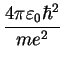 Bohr Radius Bohr Radius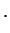 |
(292) |
The radial eigenfunctions for the bound states are
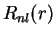 |
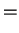 |
![$\displaystyle -\frac{2}{n^2}\sqrt{\frac{(n-l-1)!}{[(n+l)!]^3}}
e^{-r/na_0}\left...
...r}{na_0}\right)^lL^{2l+1}_{n+l}\left(\frac{2r}{na_0}\right),\quad
l=0,1,...,n-1$](img1248.png) |
(293) |
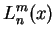 |
 |
 generalized Laguerre polynomials generalized Laguerre polynomials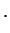 |
|
The wave functions of the bound states of the hydrogen atom (i.e. the attractive Coulomb potential (4.68))
are therefore given by the product of radial and angular part according to our separation ansatz
(4.61),
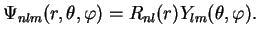 |
|
|
(294) |




Next: The Angular Momentum
Up: The Hydrogen Atom
Previous: The Angular Part
Contents
Tobias Brandes
2004-02-04
![$\displaystyle \frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2
\frac{\partial...
...)}{\partial r}\right)+\frac{2m}{\hbar^2}[E-V(r)]R(r)
-\frac{l(l+1)}{r^2}R(r)=0.$](img1239.png)
![$\displaystyle \frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2
\frac{\partial...
...)}{\partial r}\right)+\frac{2m}{\hbar^2}[E-V(r)]R(r)
-\frac{l(l+1)}{r^2}R(r)=0.$](img1239.png)
![]() and the radial eigenfunctions
here but present the result: For bound states where the electron is bound to the attractive
potential, the possible eigenvalues
and the radial eigenfunctions
here but present the result: For bound states where the electron is bound to the attractive
potential, the possible eigenvalues ![]() are labeled by a quantum number
are labeled by a quantum number ![]() ,
,
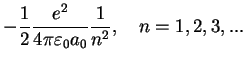 Lyman Formula
Lyman Formula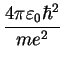 Bohr Radius
Bohr Radius![$\displaystyle -\frac{2}{n^2}\sqrt{\frac{(n-l-1)!}{[(n+l)!]^3}}
e^{-r/na_0}\left...
...r}{na_0}\right)^lL^{2l+1}_{n+l}\left(\frac{2r}{na_0}\right),\quad
l=0,1,...,n-1$](img1248.png)
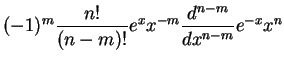 generalized Laguerre polynomials
generalized Laguerre polynomials