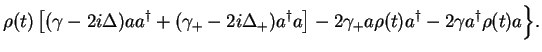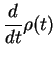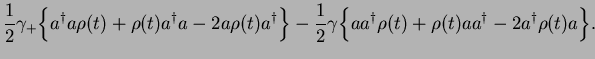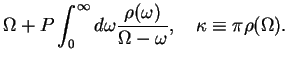Next: Expectation Values (RWA Model)
Up: Master Equation II: the
Previous: Rates and Energy Shift
Contents
Index
Using these definitions, we can now write
We write
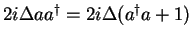 and obtain
and obtain
This can be further re-arranged into
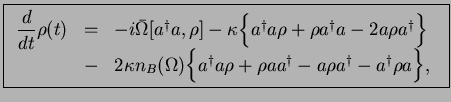 |
|
|
(48) |
where
Remarks
- This is the `standard' Master equation for the damped harmonic oscillator, as discussed in
many text books and used for many applications.
- Modifications appear if one uses the non-RWA model Hamiltonian instead of the RWA Hamiltonian.
- Eq.(7.48) is, of course, not exact because we have used 2nd order perturbation
theory (in the system-bath coupling
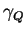 ), and the Markov approximation.
), and the Markov approximation.
- The oscillator energy
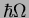 is renormalised due to the
coupling to the environment. The renormalised frequency
is renormalised due to the
coupling to the environment. The renormalised frequency
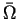 is temperature
independent.
is temperature
independent.
- The integral for the renormalised frequency
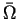 may diverge, depending on
the form of the spectral density
may diverge, depending on
the form of the spectral density
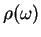 , Eq.(7.37), in which case this
theory breaks down. We will make this statement more precise below.
, Eq.(7.37), in which case this
theory breaks down. We will make this statement more precise below.
- One can show that the Master equation Eq.(7.48)
(and its non-RWA analogon, model 1) is indeed `wrong'
in the sense that there is an exact solution for the density operator
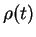 within the same model,
which is different from the solution of Eq.(7.48). This again will be discussed
below.
within the same model,
which is different from the solution of Eq.(7.48). This again will be discussed
below.
- Comparing the exact
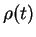 with that obtained from Eq.(7.48), one
could now discuss the `validity of the entire Master equation approach'. However,
the damped harmonic oscillator is (with very few exceptions) the only
quantum dissipative system where an exact solution exists.
with that obtained from Eq.(7.48), one
could now discuss the `validity of the entire Master equation approach'. However,
the damped harmonic oscillator is (with very few exceptions) the only
quantum dissipative system where an exact solution exists.





Next: Expectation Values (RWA Model)
Up: Master Equation II: the
Previous: Rates and Energy Shift
Contents
Index
Tobias Brandes
2004-02-18
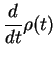
![$\displaystyle -i[\Omega a^{\dagger}a,{\rho}(t)] %%\nonumber\\
-\frac{1}{2}\Big...
...2 i \Delta_+)a^{\dagger} a
+ (\gamma + 2i \Delta) a a^{\dagger}\right]{\rho}(t)$](img186.png)