




Next: `Direct' and `Exchange' Operators
Up: The Variational Principle for
Previous: The Variational Principle for
Contents
Index
We use the Hamiltonian Eq. (IV.2.1),
The energy functional now depends on the
 wave functions
wave functions
 ,
,
 ,
,
![$\displaystyle F[\Psi]= F[\psi_{\nu_1},...,\psi_{\nu_N}]=F[\{\psi_{\nu_i}\}].$](img665.png) |
|
|
(3.14) |
The definition of the functional derivative is not more complicated than in the one-component case,
![$\displaystyle \frac{\delta F[\Psi]}{\delta \Psi}\equiv
\lim_{\varepsilon\to 0} ...
..._{\nu_i}+\varepsilon \cdot \delta \psi_i\}] -F[\{\psi_{\nu_i}\}]}{\varepsilon},$](img666.png) |
|
|
(3.15) |
where we now have
 independent `deviations'
independent `deviations'
 from the functions
from the functions
 . We furthermore want to ensure that all single particle states
. We furthermore want to ensure that all single particle states
 are normalised. Therefore, we introduce our functional
are normalised. Therefore, we introduce our functional
![\bgroup\color{col1}$ F[\Psi]$\egroup](img641.png) with
with
 Lagrange multipliers
Lagrange multipliers
 ,
,
![$\displaystyle F[\Psi] \equiv \langle \nu_N,...,\nu_1 \vert\hat{H}\vert\nu_1,...,\nu_N\rangle_A
+ \sum_{i=1}^N \lambda_i[ \langle \nu_i\vert\nu_i\rangle -1 ].$](img670.png) |
|
|
(3.16) |
We have calculated the energy expectation values already in Eq. (IV.2.5) and Eq. (IV.2.9),
The individual terms are simply calculated:
The term from the interaction
 yields
yields
We can use the symmetry property (Exercise: proof!)
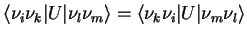 |
|
|
(3.20) |
to simplify things by using, e.g.,
 and changing the summation indices
and changing the summation indices
 ,
,
 such
that
such
that
where again in the `
 ' term we have swapped indices, and
' term we have swapped indices, and
 means that there are two terms which
are the hermitian conjugates of the two others.
means that there are two terms which
are the hermitian conjugates of the two others.





Next: `Direct' and `Exchange' Operators
Up: The Variational Principle for
Previous: The Variational Principle for
Contents
Index
Tobias Brandes
2005-04-26




![$\displaystyle \frac{\delta F[\Psi]}{\delta \Psi}\equiv
\lim_{\varepsilon\to 0} ...
..._{\nu_i}+\varepsilon \cdot \delta \psi_i\}] -F[\{\psi_{\nu_i}\}]}{\varepsilon},$](img666.png)
![$\displaystyle F[\Psi] \equiv \langle \nu_N,...,\nu_1 \vert\hat{H}\vert\nu_1,...,\nu_N\rangle_A
+ \sum_{i=1}^N \lambda_i[ \langle \nu_i\vert\nu_i\rangle -1 ].$](img670.png)
![$\displaystyle \sum_{i=1}^{N}\langle\nu_{i}\vert\hat{H}_0\vert\nu_{i}\rangle + \...
...j}\rangle
-\langle\nu_{i}\nu_{j}\vert U_{ij} \vert\nu_{i}\nu_{j}\rangle \right]$](img672.png)
![$\displaystyle \sum_{i=1}^N \lambda_i [ \langle \nu_i\vert\nu_i\rangle -1 ].$](img673.png)

![$\displaystyle \lim_{\varepsilon\to 0} \frac{1}{\varepsilon}
\left[ \sum_{i=1}^{...
..._i\rangle-
\sum_{i=1}^{N}\langle\nu_{i}\vert\hat{H}_0\vert\nu_{i}\rangle\right]$](img675.png)
![$\displaystyle \sum_{i=1}^{N} \left[\langle \delta\nu_i\vert\hat{H}_0\vert\nu_{i}\rangle + \langle \nu_i\vert\hat{H}_0\vert\delta\nu_{i}\rangle\right].$](img676.png)
![$\displaystyle \frac{\delta}{\delta \Psi}
\frac{1}{2}\sum_{ij}\left[\langle\nu_{...
...\nu_{j}\rangle
-\langle\nu_{i}\nu_{j}\vert U \vert\nu_{i}\nu_{j}\rangle \right]$](img677.png)
![$\displaystyle \frac{1}{2} \sum_{ij}\Big[\langle \delta \nu_{j}\nu_{i}\vert U\ve...
...{j}\rangle
+ \langle\nu_{j}\nu_{i}\vert U\vert\nu_{i}\delta \nu_{j}\rangle\Big]$](img678.png)
![$\displaystyle \frac{1}{2} \sum_{ij}\Big[\langle \delta \nu_{i}\nu_{j}\vert U\ve...
...j}\rangle
+ \langle\nu_{i}\nu_{j}\vert U\vert\nu_{i}\delta \nu_{j}\rangle\Big].$](img679.png)
![$\displaystyle \frac{\delta}{\delta \Psi}
\frac{1}{2}\sum_{ij}\left[\langle\nu_{...
...\nu_{j}\rangle
-\langle\nu_{i}\nu_{j}\vert U \vert\nu_{i}\nu_{j}\rangle \right]$](img677.png)
![$\displaystyle \sum_{ij}\Big[\langle \delta \nu_{j}\nu_{i}\vert U\vert\nu_{i}\nu...
...j}\rangle
- \langle\nu_{i}\nu_{j}\vert U\vert\nu_{i}\delta \nu_{j}\rangle \Big]$](img682.png)
![$\displaystyle \sum_{ij}\Big[\langle \delta \nu_{j}\nu_{i}\vert U\vert\nu_{i}\nu...
...- \langle \delta \nu_{j}\nu_{i}\vert U\vert\nu_{j}\nu_{i}\rangle + (H.c.)\Big],$](img683.png)